Solving a Rubik's pocket cube with a graph database
17 mars 2017 · 5 min read
A pocket cube can have 3 674 160 different positions. For a “No-SQL” database, it’s a piece of cake.
Neo4j is a graph database. In this tool, each node could be a cube position, and eges from one node to another could be a move.
As this software can find the shortest path between two nodes, could it solve the cube with “god move” i.e. 14 at most from a given position ?
The answer is : yes, within a few milliseconds.
Here is how to do.
Cube representation
First of all, we have to code the cube description. Here is a way to do :
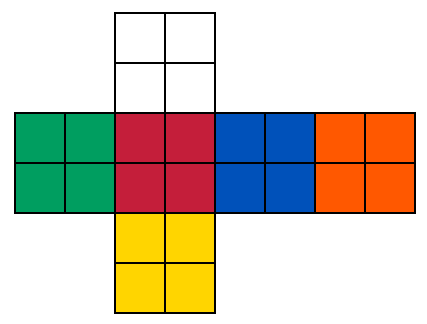
This is the same as :
// b=blue T=top
// w=white F=front
// o=orange D=down
// r=red B=back
// y=yellow L=left
// g=green R=right
//
// --- ----- ---
// |w|w| |0 |1 | | T |
// |w|w| |2 |3 | | |
// --- --- --- --- ----------------------- ---------------
//|g|g|r|r|b|b|o|o| |4 |5 |6 |7 |8 |9 |10|11| | L | F | R | B |
//|g|g|r|r|b|b|o|o| |12|13|14|15|16|17|18|19| | | | | |
// --- --- --- --- ----------------------- ---------------
// |y|y| |20|21| | D |
// |y|y| |22|23| | |
// --- ----- ---
The position of a cube is written into an array of 24 elements :
// the solved cube can be coded as it :
$position = array(
'w','w','w','w',
'g','g','r','r',
'b','b','o','o',
'g','g','r','r',
'b','b','o','o',
'y','y','y','y'
);
// or this way if we write numbers instead of colors :
$position = array(
0,0,0,0,
2,2,4,4,
3,3,5,5,
2,2,4,4,
3,3,5,5,
1,1,1,1
);
However, this representation has a downside : imagine a solved cube in front of you. Its position is 000044335522443355221111. Turn the whole cube in the space to have another side color in front of you. It will be for example 000033552244335522441111. But this is the same cube ! We can’t have 2 IDs ! We can rotate the whole cube 4 times on the 6 faces. There are 24 different notations for the same cube.
To reduce this number to one, we can sort thoses 24 notations by alphabetic order : 000022443355224433551111 | 000033552244335522441111 | 000044335522443355221111...
The first element is used as the key to identify the position (ID).
The ID for the solved cube is : 000022443355224433551111.
Then, we can code the following methods :
- domove : to play a move, i.e. turn a face like this :
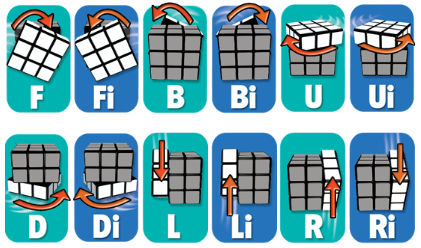 Letters mean : Front, Back, Up, Down, Left, Right. Moves are done clockwise. A “i” is counter clockwise. In the program, moves are done by swaping the array elements. For example, a move up (U), will change the elements 0 to 3 and 4 to 11 (refer to the description upper).
Letters mean : Front, Back, Up, Down, Left, Right. Moves are done clockwise. A “i” is counter clockwise. In the program, moves are done by swaping the array elements. For example, a move up (U), will change the elements 0 to 3 and 4 to 11 (refer to the description upper). - undomove : to undo a move (just “domove Li” to undo L ;))
- setpos : to set a given position to the cube.
- rotx : do moves U, Di, and your cube has rotated a 1/4 turn.
- roty : do moves Li, R.
Generating all possible positions
Or how to generate 3 674 160 ids for all the positions of the cube and the links between them.
Here is the algorithm :
we start from the solved cube
save that this position is to do
while we have positions to do:
get the ID (A) of the position
add ID (A) to the nodes if not already added
for each 12 possible moves:
play the move
add the ID (B) of this new position to the nodes if not already added
save that this position (B) is to do if not already done
save the edge A->B in the edges file
undo the move
save the position ID (A) as done
Here is the progress :
After around twenty hours, we have two CSV files of 110 and 585 Mb.
nodes.csv :
pos:ID;:LABEL
000022443355224433551111;Cube
004441330522413305225511;Cube
004441330522330522415151;Cube
000244351522343052411351;Cube
000533512244312501344215;Cube
000533512244343125011452;Cube
000433502524343522411151;Cube
002234051524305312413451;Cube
021425330515430423125014;Cube
And bingo ! there are 3 674 160 nodes ! this number has never been coded. So it really works. The algorithm is correct.
We have the edges.csv file :
:START_ID;:END_ID;:TYPE
000022443355224433551111;004441330522413305225511;MOVE
000244351522343052411351;004441330522330522415151;MOVE
000533512244312501344215;000533512244343125011452;MOVE
000433502524343522411151;002234051524305312413451;MOVE
004550212433143501341225;021425330515430423125014;MOVE
000233551524341423112054;001232540524305123113454;MOVE
021425330405130211235544;031225351045130414235240;MOVE
002341441432535535011022;024552131053404523412130;MOVE
001142542432013435355120;002341441432015355352120;MOVE
You have noticed that i had written headers to import to Neo4j.
Import files to Neo4j
If we have a temporary database, we can delete it :
sudo rm -rf /data/databases/*
Change directory to our CSV files :
cd /var/lib/neo4j/import/data
Import files to Neo4j :
/var/lib/neo4j/bin/neo4j-admin import \
--into /data/databases/graph.db \
--nodes nodes.csv \
--relationships edges.csv \
--delimiter ";" \
--array-delimiter "-" \
--quote "'"
It is really fast ! 3,6 millions nodes and 10,6 millions of edges imported in 1 minute and 8 seconds !
IMPORT DONE in 1m 8s 438ms.
Imported:
3674160 nodes
10631005 relationships
3674160 properties
Peak memory usage: 79.57 MB
NB : you have to restart Neo4j : sudo service neo4j restart.
Solving the cube
Or finding the shortest path between two nodes.
Thanks to a graphical user interface coded in Javascript for example, we let the user describe his cube position. We generate the ID of his position, for example 002140534352524214031513. We ask Neo4j to find the shortest path between it and the solved ID which is 000022443355224433551111. Here is the Cypher query :
MATCH (c1:Cube), (c2:Cube), p = shortestPath((c1)-[m:MOVE*]-(c2))
WHERE c1.pos="002140534352524214031513" AND c2.pos="000022443355224433551111"
RETURN p
The results comes in 0.08 seconds :
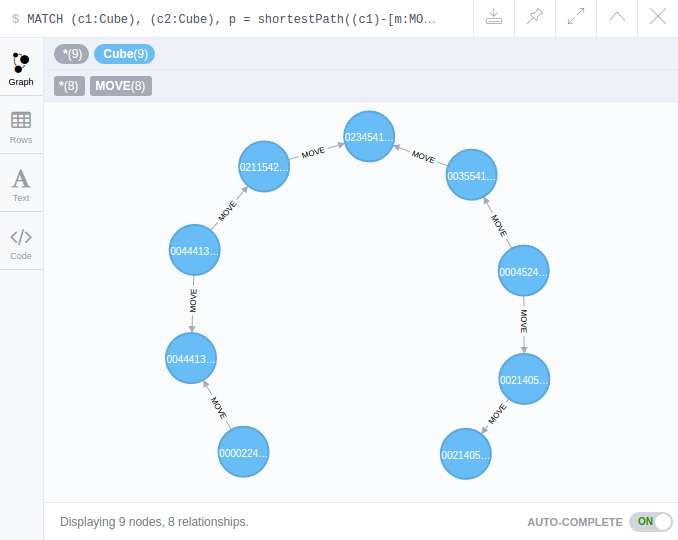
NB : A directed link is not necessary but in Neo4j links are directed. We don’t care about the directions. A move from node (A) goes to (B) and (B) goes to (A).
We could’nt add the move name to the edges [MOVE] because we have simplified 24 notations to 1.
So to find the move name (F, B, D, Di, L…) between two nodes, we can do like this :
We start from the given position, we play the 12 possible moves, and we check each ID of the new position, to match with the ID of the next node of the solution got from Neo4j.
I made some tests. Cube is really solved at most in 14 moves !
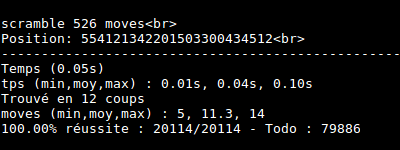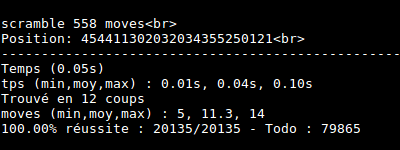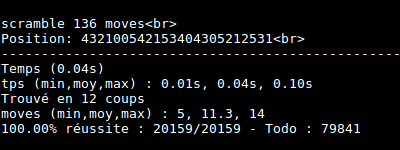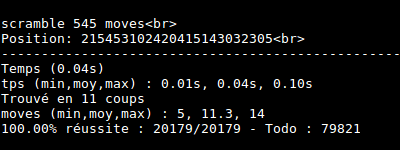
Conclusion
Try the Android Cube Solver app. Have fun.